Universe is an ambitious system.
The first consequence of the computational nature of the universe is that it creates complexity, as life.
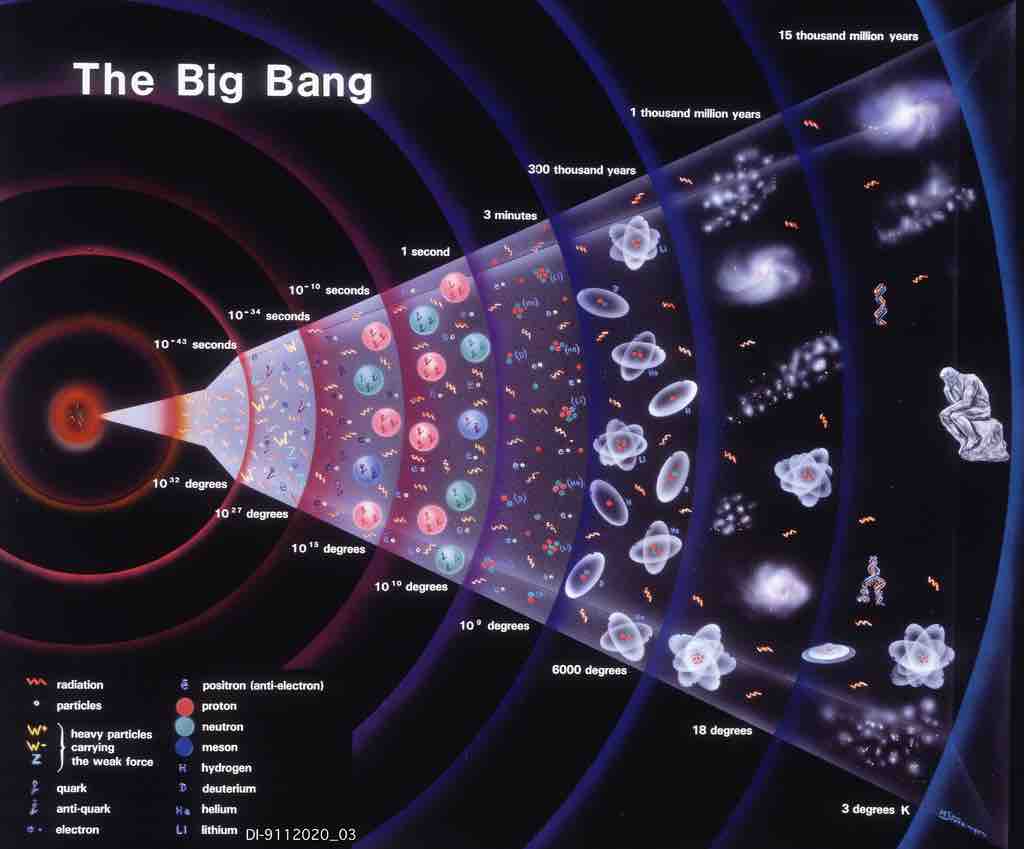
Originally the universe was quite simple, but now it is no longer. Astronomers and cosmologists confirm that the universe at the Big Bang was not complicated at all. It was very hot and almost the same at every point. Indeed the initial state was characterized by a great regularity, symmetry and **simplicity.
Nowadays things are hugely different: think all the planets, stars, galaxies and clusters of galaxies. The universe is highly asymmetric. Ludwig Boltzmann, an Austrian physicist, asserted that the complexity of the universe comes from the case. He was the first whom spoke of monkeys hitting keys at random on a keyboard.

###Algorithmic information and algorithmic probability.
Define complexity is not easy at all. Asking how measure complexity is like asking measure Physics. There are many measurable quantities in physics such as distance, temperature, pressure, but the Physics itself is not a measurable quantity.
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information. Algorithmic information can be considered as a measure of how difficult is to represent a string of bits using a computer. In particular, the algorithmic information contained in a string, is the length (in bits) of the smallest program which produces that string as output.
Algorithmic information is a fascinating concept, based on the universality and translatability of programming languages. It allows to express in a compact way a string of bits which contains a mathematical regularity. The smallest program which is capable of producing a string of bits can be also thought of as a compressed representation of the string of bits. Algorithmic information has been proposed as a measure of algorithmic complexity, because of a string with high algorithmic information can be produced with little effort. As a consequence, it is greater for small programs.
Another interesting concept for complexity evaluation is the Algorithmic probability. In algorithmic information theory, algorithmic probability is the probability that a program generated in a random way, ie wrote by a monkey, gives as output the desired result.
###Computational complexity The computational complexity is the number of elementary logical operations which must be made in the course of the computation. A relative concept is the spatial complexity, which is equal to the number of bits used during the computation. But computational complexity is not a measure of the complexity more than a measure of the effort. Indeed there are programs that require a lot of time and space but do not produce anything complex.
###Logical depth
Traditional definition of complexity is a trade off between information and effort: 1. describe how is difficult to describe something (algorithmic information) 2. describe how is difficult to do something (computational complexity) 3. describe the degree of organization of the system 4. describe quantitative ideas not associated with the complexity (self organization, adaptive systems)
Charles Henry Bennett, introduced the concept of Logical depth: he first identified the most plausible explanation for a string of bits or a data set with the smallest program that is able to produce it. Then, Bennett looked at the computational complexity of this small program. He called this quantity the logical depth. In simply words, logical depth is nothing but that the computation time of the algorithm with the shortest length.
###Thermodynamic depth and effective complexity
Instead of looking at the more plausible way with which a string of bits is produced by the shortest program, we can look directly at the more plausible way with which a physical system can be produced. Then, instead of using the computational complexity (the number of logical operations), we look at the amount of physical resources necessary to produce that physical system.
In particular, the physical resource we are interested in is the entropy. A physical system is composed of: 1. entropy: made of unknown and causal bits 2. negentropy: consists of known bits, structured and useful
Thermodynamic depth of a physical system is the number of useful bits that are needed to assemble the system.
The logic and thermodynamics depth are not the only elements to quantify certain aspects of complexity. Another one is the so called effective complexity, a measure of the amount of the regularity of a system. It is a measure of complexity simple and elegant. Each physical system has associated with it a certain amount of information, a quantity required to describe its physical state with the accuracy allowed by quantum mechanics. This quantity is divided into two parts: one part which describes the regularities and the other one which describes its causal component. Obviously, determining the effective complexity involves an assessment of what thing constitutes a regular thing and what is not. This is equivalent to asking the question how do you determine if a bit is important (regular) or not (randomness)? One way to determine its contribute to complexity; flip the bit and see what happens. If changing the bit has a significant impact, then it is important; if it does not change much, it is not important. In general, the importance of a bit of a living being, can be assessed by considering its effects in obtaining energy and in making copies of itself.
###Why the universe is so complex? To assess the complexity of the universe, we need start from the standard cosmological model. In this model, it is stated that there is not enough matter in the universe to ensure that its expansion will stop and produce a big crunch. The Universe will expand forever.
The first information processing revolution was the Big Bang itself. The observations suggest that the early universe was very simple as far as we can tell, there was only one possible initial state and it was the same everywhere.
If there was only one possible state at time T0, the universe contained zero bits of information and its logic depth, thermodynamics depth and effective complexity were zero. Then the universe began to compute. After a Planck time (10 to the -44), the universe contained a bit of information. The amount of computation that can be made with only one bit is only one operation. For which the actual complexity and thermodynamics depth could not be greater than a single bit, and the logic depth can not be greater than one bit. The monkeys had beat only a bit.
As the universe expands, the number of bits within the time horizon grow as the number of transactions. The maximum depth is limited by the number of logical operations, and the actual complexity and thermodynamics depth are limited by the number of bits available. The universe continued to grow in complexity but was still relatively simple. The monkeys continued to beat. And what was the universe computing in those first instants? Itself, its own behavior.
Charles Bennett defined the early universe an ambitious system: it was initially simple, but it is able to generate large amounts of complexity over time.
Quantum fluctuations can lead to situations in which a bit 0 stands for an energy density below the average, while 1 stands for energy density above the average. Recall that the universe computes in overlapping bits, and the information is interpreted by the laws of physics. Information spreads until it decoherence. The next state is crucial. Gravity responds to the presence of energy. Where the energy density is high, the structure of space-time begins to curve a little.
The Gravity responds to fluctuations of energy by condensing the matter. When qubits are no longer consistent, gravity begins to behave in a classical way. In addition to creating the earth on which we walk, gravitational aggregation also provides the materials necessary to generate complexity. As matter condenses, it becomes free to be used. Gravity is responsible for the calories we ingest, planets and galaxies. This revolution was followed by others: life, sexual reproduction, brain, language, numbers, writing, printing, computers.
A computation is merely flipping bits in a systematic way. To prove that something is able to make a universal computation, all we have to do is prove that it can perform AND, NOT, OR and COPY operations. The chemical reactions, for example, are universal computation.
###Many-worlds interpretation, again The universe that we look around us corresponds to only one of all the possible decoherent stories: this is, what we look out the window is only one component of states superposition which is the total quantum state of the universe. The other components of this state correspond to other worlds, worlds in which launches of the quantum dice constitutes a multi-universe. Our life is the result of countless launches of the quantum dice, about 10 to the 92 to be exact.Nevertheless, the total quantum state of the universe remains simple, the universe began with a simple state and evolves according to simple laws.

How long this computation will continue in the universe? Observations tell us that the universe will expand forever, and since it will expand forever, the number of operations and the number of bits available inside the event horizon will continue to grow. Even the entropy will continue to grow, but at a lower rate. The problem is that while the amount of free energy increases, the amount of free energy per cubic meter decreases, ie density decreases.
###Further Information
Programming the Universe, by Seth Lloyd
Ultimate physical limits to computation, by Seth Lloyd
The Universe as Quantum Computer, by Seth Lloyd
Quantum Computing, Wikipedia.org
The Road to Reality: A Complete Guide to the Laws of the Universe, by Roger Penrose
Dance of the Photons: From Einstein to Quantum Teleportation